A space or a region which is covered by a parallelogram in a two-dimensional plan is known as a parallelogram. A parallelogram area can be defined as the total number of square units that can fit in it and also which can be measured in square units. In a parallelogram, the sum of the adjustment angle is 180 degrees. The different shapes in geometry that we know have different properties from each other. The perimeter and the area of these different shapes also differ. We can define parallelogram in a more clear manner as a quadrilateral whose two pairs have parallel sides. The length of the opposite side in a parallelogram is equal along with the opposite angles also as parallel. Now the area of the parallelogram can be more clarified as space that is occupied by the two-dimensional plan. In this article, we will discuss what is a parallelogram and the area of the parallelogram, and different methods to calculate the area of a parallelogram in detail.
Parallelogram
As already mentioned in the above paragraph the parallelogram can be defined as a closed figure with the two pairs of sides as parallel. Also, we know that the opposite sides are equal as well in a parallelogram so the opposite sides and angles congruence is a consequence of the euclidean parallel postulate.
A parallelogram can be obtained from many different figures, as discussed below:
- From an automedian triangle, we can obtain the figure of a parallelogram. These triangles are in equal proportion as that of their sides.
- A Varignon can form the parallelogram: the parallelogram’s vertices are the midpoints of its sides of a varignon.
- Ellipse of parallelograms tangent: the two diameters are congruent in an ellipse if the line of tangent is equal to the other diameter.
- The faces of a parallelepiped also form the parallelogram.
Three main types of bifurcation are done in parallelogram these are as:
- Triangle
- Square
- rhombus
In a parallelogram, the diagonals intersect each other.
Click here – What is the Work of Digital Marketing?
Area of Parallelogram
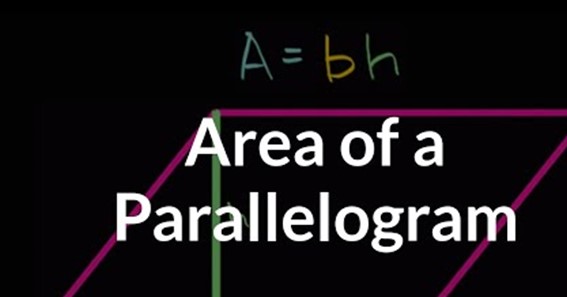
In the above topics, we have learned about parallelograms. In this topic, we will know what is the area of a parallelogram. The total number of unit squares that can fit inside a parallelogram is the area of the parallelogram. By multiplying the altitude with the base we can crack the area of parallelogram. These two entities mentioned above (base and height) are perpendicular to each other. Thus we can say that the area of parallelogram can be written as :
area= height(h)*base(b).
Here the alphabet h is the height and the alphabet b is the base.
There are some more methods by which one can easily find the area of the parallelogram that is by applying the following ways which are mentioned below in this article:
As we already know, the property of a parallelogram is that its diagonals intersect each other. So if the area of the diagonals is known to us so by this method also the area of the whole parallelogram can be calculated. We can calculate the area of the parallelogram also by the help of the sides. Even if we don’t know the height then also we can find out the area of the parallelogram only by knowing the adjutant sides and the angle between them. The area of the parallelogram can be calculated in another manner, that is we can find the area if the height is known to us. As above the area was found even though we didn’t know the height the same way an area could be found even if we don’t know other entities but we know the height.
Click here – How to Improve Your Dog’s Wellness Routine
To Know Some Great Stuff Do Visit EagerClub
To Know Some Great Stuff Do Visit EarthCycle
To Know Some Great Stuff Do Visit EkSankalpJob